最优Topn算法
25 Oct 2009在大量的数据记录中,依据某可排序的记录属性(一般为数字类型),找出最大的前N个记录,称为 TopN问题。这是一个常常遇到的问题,也是一个比较简单的算法问题,却很少能有人能写出最优化的 topn算法。本文对常见的TopN算法,进行分析比较,最后给出最优的TopN算法:基于小根堆的筛选 法.
2.问题定义
为了方便。我们把问题具体化:要求使用C语言来实现函数,在一个大小为m的,无序的整数数组中选 取最大的n个整数。即,问题定义为一个函数的实现:
int * topn(int *pdata, int m,int *ptop, int n);
其中,pdata指向保存大量整数的内存,整数的个数为m,要求函数把前n个最大的整数保存到ptop指向的内存中,显然满足m≥n≥0 。 同时假定n<m/2, 因为当n如果超过半数,可以问题转换为排除n−m/2个最小的整数----这种转换减少了问题规模。
我们虽然假设的数据类型为整数,其他任意的数据类型,只要其数据是可以排序的,都可以根据这里的 算法,写出对应的算法实现。同样,我们虽然假定输入数据的方式为数组,实际输入的方式可以是任意 其他方式(如文件,数据库等)。
3.算法介绍
3.1 算法1 完整排序法
对pdata中的数据,进行内部排序,然后选取前n个整数放到ptop中。如果使用较高效率的内部排序 算法(如:快速排序,堆排序),复杂度为m∗log2m, 使用这种算法,结果数据是自然从大到小排序的。
3.2 算法2 基于有序数组的筛选法
保持ptop中的结果数组有序,即满足ptop[0]≥ptop[1]≥...≥ptop[n−1] ,遍历pdata中的数 据,如果发现当前整数大于ptop[n-1]就把数据插入到合适位置,以保持ptop中的仍然有序。算法复 杂度为. m∗n, 使用这种算法,结果数据是从大到小排序的。 显然,只从理论上的复杂度考虑,就可以看出来:当n较小的时候,算法2有较高的效率。但当n较大 的时候,算法1会有较高的效率。
仔细分析算法2, 保持ptop中数据有序的目的,就是每次能找到最小的值,在有序数组中插入一个新元 素,最坏需要n次操作才能保持数组有序。其实要快速找到最小的值,使用小根堆更合适,因为中堆中 每次插入一个元素,最坏只需要log2n 次操作,根据这个思路产生下面的算法3。
3.3 算法3 基于小根堆的筛选法。
使用大小为n的小根堆保存结果集,最小项为堆的根节点ptop[0],遍历pdata中,如果当前数据大于 ptop[0],则用当前数据替换根节点,并对根节点SiftDown操作,保持结果集仍然为小根堆。算法复杂度, 只有m∗log2n .- 更多关于小根堆的介绍,请看后面。显然,m∗log2n<m∗log2m<m∗n,所以,算法3的复杂度最低。
这种算法,生成的结果数据是没有排序的。因为结果已经保存最小根堆种,如果需要排序,只需要完成 常规堆排序流程的后半部分,排序需要的复杂度只有n。
4 实际测试结果
测试环境:
OS: Debain Linux kernel 2.6.26
C Complier: gcc 4.3.4
MEM: 768m
CPU: Intel(R) Pentium(R) 4 CPU 2.40GHz
测试方法:
随机生成40万个整数,(m = 400000),求最不同n值下,各个算法的实际测试结果
| - | 算法1完整排序法(m∗log2m) | 算法2基于有序数组的筛选法(m*n) | 算法3基于小根堆的筛选法,排序(m∗log2n) | 算法3基于小根堆的筛选法,不排序(m∗log2n+n) |
|---|---|---|---|---|
| Top 10 | 190ms | <1ms | <1ms | <1ms |
| Top 100 | 180ms | 10ms | <1ms | <1ms |
| Top 1000 | 190ms | 30ms | <1ms | <1ms |
| Top 5000 | 190ms | 470ms | 10ms | 10ms |
| Top 10000 | 180ms | 1650ms | 20ms | 20ms |
| Top 50000 | 180ms | 25820ms | 70ms | 40ms |
| Top 100000 | 190ms | 77360ms | 120ms | 70ms |
| Top 200000 | 190ms | 201900ms | 180ms | 110ms |
5 算法分析
- 在任何情况下,算法3都是最优的。但算法3的实现较复杂。
- 如果不想实现复杂的算法3,如果n相对于m很小,可以选择算法2
- 如果不想实现复杂的算法3, 如果n比较大,例如:接近了m/2, 可以选择算法1
- 如果不要求结果排序,算法3更有优势。
- 算法1和算法2,结果自然就排号顺序了。是否要求排序与其时间花费无关。
根据理论复杂度和实际的测试结果,更有下面的结论。当m值固定,n的变化区间为[1,m/2],三种算法消耗时间随n变化的曲线,如下面的图示意。
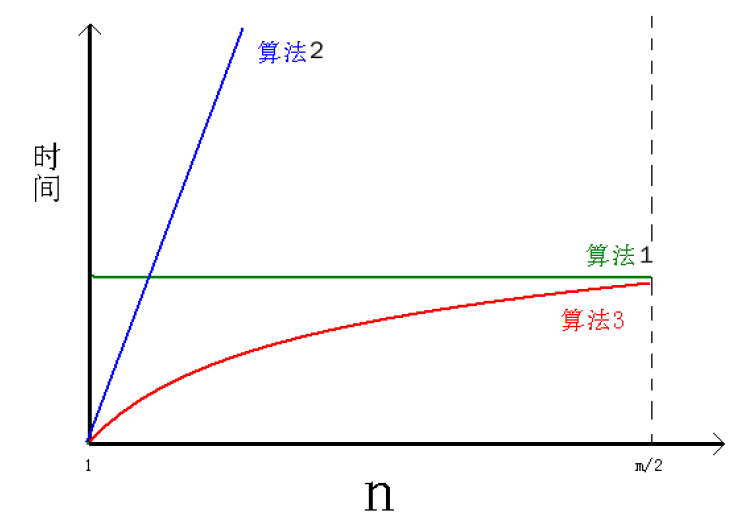
相应的,当n固定,m的变化区间为[2*n, ∞ ), 三种算法消耗算法随m变化的曲线,如下面的图示意。
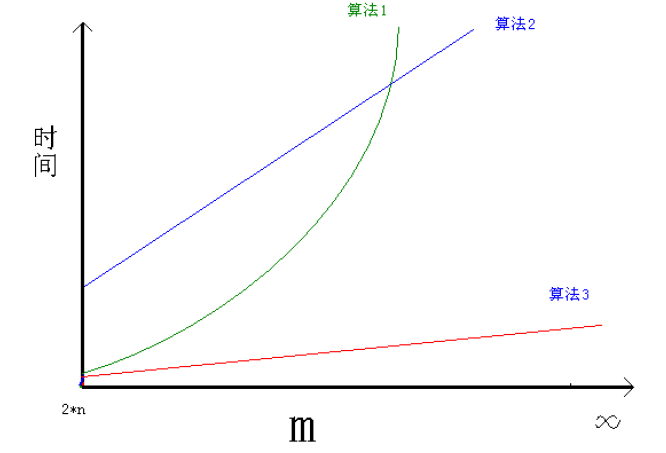
6 算法实现
6.1 算法1 实现
使用标准c语言库支持的qsort,直接就可以实现。
//用于比较操作的函数
static int cmpint(const void *p1, const void *p2)
{
return *((int *)p2) - *((int *)p1);
}
//算法实现
int * topn1(int *pdata, int m,int *ptop, int n)
{
qsort(pdata, m, sizeof(int),cmpint);
memcpy(ptop, pdata, n*sizeof(int));
return ptop;
}
注意:如果自己实现qsort算法,会有一定效率的提高。但代码级的优化,这里不会对效率产生本质的影响。
6.2 算法2 实现
比较简单,源代码如下
int *topn2(int *pdata,int m,int *ptop,int n)
{
int i;
for(i=0;i<m;i++)
{
//判断当前结果集的大小(数组的长度)
int t = (i+1<n) ? (i+1):n;
if(i>=n && pdata[i] <= ptop[n-1])
continue;
int j=t-1;
for(;j>=1 && pdata[i]>ptop[j-1];j--)
ptop[j] = ptop[j-1];
ptop[j] = pdata[i];
}
return ptop;
}
注意:如果使用监视哨等优化手段,可以减少循环的判断条件。但这种代码级别的优化,这里不会对效 率产生本质的影响。
6.3 算法3 实现
6.3.1 小根堆概念定义
小根堆精确定义:数组 x1..n, 如果满足:∀i∋[2,n], x[i/2]≤x [i].就说明,这个数组就是小根堆.为了下面描述方便,我们定义对数组x[1..n]的子数组x[u..v],( 1≤u≤v≤n ),如果满足: ∀i∋[2l, u],x[i/2]≤x [i], 就说明:x整个数组的[u..v]部分已经是小根堆了。
6.3.2 我们需要的堆操作
//如果[2..n]已经是堆了,-除了第一个元素,其他部分已经是小根堆。
//通过下面的函数把第一个元素,往后交换,把整个数组变成堆。
void siftdown_head(int *pheap,int n)
{
pheap --; //这样作是让第一个元素的索引变成1, pheap[0]永远不会被访问到
int t = pheap[1];
int i =1;
int c = i*2;
while(c<=n)
{
if(c<n && pheap[c]>pheap[c+1])
c++;
if(pheap[c] < t)
{
pheap[i] = pheap[c];
i = c;
c = 2*i;
}
else
break;
}
pheap[i] = t;
}
//如果除了最后一个元素外,其他部分[1..n-1]已经是堆了,
//通过下面的函数,把最后一个元素往前交换,把整个数组调整成堆
void siftup_rear(int *pheap,int n)
{
pheap --;
int t = pheap[n];
int i;
for(i=n; i>1;)
{
int p = i/2;
if( pheap[p] > t)
pheap[i] = pheap[p];
else
break;
i=p;
}
pheap[i] =t;
}
更多关于堆的概念,可以在网上找到。最常见的应用是使用堆来实现高效率的优先级队列(如c++的标 准模板库)。在本文应用场景中,也可以把保存topn结果的数组看成是优先级队列,因为我们总是选择 数值最小的值,进行出队操作(数值越小,优选级越大)。最后,队列中剩余的,自然就是数值较大的 topn结果。
6.3.3 算法实现
int * topn3(int *pdata, int m,int *ptop, int n)
{
ptop[0] = pdata[0];
int i;
for(i=1; i<n;i++)
{
ptop[i] = pdata[i];
siftup_rear(ptop,i+1);
}
for(i=n;i<m;i++)
{
register t = pdata[i];
if(ptop[0] >= t)
continue;
ptop[0] = t;
siftdown_head(ptop,n);
;
}
//如果不需要把结果排序,下面的这段循环可以乎略掉
for(i=n-1; i>=1;i--)
{
int t = ptop[i];
ptop[i] = ptop[0];
ptop[0] = t;
siftdown_head(ptop,i);
}
return ptop;
}